Пробный вариант контрольной, 2-ой семестр.
Найти 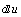 и
и 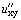 , если
, если 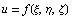 , где
, где  .
.
Преобразовать уравнение 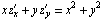 к полярным координатам
к полярным координатам 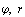 , полагая
, полагая  .
.
Представить функцию  формулой Тейлора третьего порядка в окрестности т. (0; 0).
формулой Тейлора третьего порядка в окрестности т. (0; 0).
Преобразовав к полярным координатам, свести к однократному интегралу

Найти площадь, ограниченную кривыми 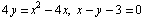 .
.
Найти объем тела, ограниченного поверхностями 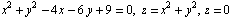 .
.
Найти точки экстремума 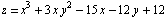 .
.
Найти глобальные экстремумы функции  на множестве
на множестве  .
.
Вычислить 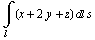 , если l - отрезок прямой между точками (1; 1; 1) и (4; 5; 6).
, если l - отрезок прямой между точками (1; 1; 1) и (4; 5; 6).
Вычислить работу, совершаемую силой 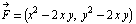 вдоль параболы
вдоль параболы 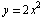 от т. (-1; 2) до т. (0,5; 0,5).
от т. (-1; 2) до т. (0,5; 0,5).
Вычислить, используя формулу Грина 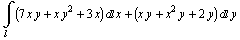 по полуокружности
по полуокружности  от т. (0; 0) до т. (-2; 0).
от т. (0; 0) до т. (-2; 0).
Найти объем пирамиды, образуемой координатными плоскостями и плоскостью, касательной к поверхности  и параллельной плоскости
и параллельной плоскости 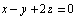 .
.
Найти площадь поверхности части конуса  , вырезанного поверхностью
, вырезанного поверхностью 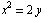 .
.
Вычислить  , где S - часть поверхности
, где S - часть поверхности 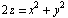 , вырезанной цилиндром
, вырезанной цилиндром 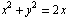 .
.
Вычислить по формуле Стокса  , где l - контур, образуемый пересечением поверхностей
, где l - контур, образуемый пересечением поверхностей  . Обход против часовой стрелки, если смотреть из начала координат.
. Обход против часовой стрелки, если смотреть из начала координат.
Вычислить, используя формулу Остроградского

через внешнюю сторону полусферы  .
.
Converted by Mathematica
September 3, 2001

![]()
![]() .
.