Тема
"Рекуррентные уравнения и динамическое программирование"

1. Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от позиции 1 до позиции N.
   Пример:
   N=4, K=2
   Возможные длины ходов:
   1,1,1
   1,2
   2,1
   Ответ: 3.
2. Покупатель имеет купюры достоинством A₁, ..., A_n, а продавец - B₁, ... , B_m. Необходимо найти максимальную стоимость товара Р, который покупатель не может купить, потому что нет возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку его достаточно.
3. У покупателя есть n монет достоинством H₁, ..., H_n. У продавца есть m монет достоинством B₁, ..., B_m. Может ли покупатель приобрести вещь стоимости S так, чтобы у продавца нашлась точная сдача (если она необходима).
4. Задана матрица натуральных чисел A[1..n, 1..m]. За каждый проход через клетку (i,j) взымается штраф A[i,j]. Необходимо минимизировать штраф и
   1. Пройти из какой-либо клетки 1-ой строки в n-ую строку, при этом из текущей клетки можно перейти в любую из 3-х соседних, стоящих в строке с номером на 1 большем;
   2. Реализовать пункт a) для перехода из клетки (1,1) в (n,m).
5. Выпуклый n-угольник, n => 3, задается координатами своих вершин в порядке обхода по контуру. Разбить его на треугольники (n-3)-мя диагоналями, не пересекающимися кроме как по концам, таким образом, чтобы
   1. Сумма их длин была минимальной;
   2. Максимальная из диагоналей имела наименьшую длину.
6. Пусть x = (a₁, a₂, ..., a_m) и y = (b₁, b₂, ..., b_n) - две заданных строки символов. Определим d(x,y) как минимальное число вставок, удалений и замен символа, которое необходимо для преобразования x в y.
   Например:
   d(ptslddf,tsgldds) = 3
   

   удаление p	вставка g	замена f
   ptslddf->	tslddf->	tsglddf->	tsgldds

   Для заданных x и y найти d(x,y).
7. Даны две строки x и y. Строка x состоит из нулей и единиц, строка y из символов A и B. Можно ли строку x преобразовать в строку y по следующему правилу: цифра 0 преобразуется в непустую оследовательность букв A, а цифра 1 - либо в непустую последовательность букв A, либо в непустую последовательность букв B?
8. Пусть известно, что для перемножения матрицы размера n*m на матрицу размера m*k требуется n*m*k операций и в результате получается матрица размера n*k. Необходимо определить, какое минимальное число операций потребуется для перемножения s матриц A₁, ..., A_s, заданных своими размерами n(i)*m(i). При этом можно перемножать любые две рядом стоящие матрицы.
   Замечание:
   n(i) - число строк в матрице A_i
   m(i) - число столбцов в матрице A_i
   n(i) = m(i+1).
9. 1. Из заданной числовой последовательности A[1..N] вычеркнуть минимальное количество элементов так, чтобы оставшиеся образовали строго возрастающую последовательность (или. что то же, найти максимальную по длине строго возрастающую подпоследовательность последовательности A).
   2. Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, одной пары соседних элементов (одного "разрыва" возрастающей подпоследовательности).
      Например: A=(1,2,3,2,4,3,4,6);
      Искомая подпоследовательность (1,2,3,2,3,4,6)
      Разрыв подчеркнут.
   3. Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, m пар соседних элементов (сформировать возрастающую подпоследовательность с m "разрывами").
10. В заданной последовательности целых чисел найти максимально длинную подпоследовательность чисел такую, что каждый последующий элемент подпоследовательности делился нацело на предыдущий.
11. Задаются число n > 1 - размерность пространства и pазмеpы М n-мерных параллелепипедов (a_i1, ..., a_in), i=1, ..., m. Паpаллелепипед может располагаться в пространстве любым из способов, при которых его ребра параллельны осям координат. Найти максимальную последовательность вкладываемых друг в друга паpаллелепипедов.
12. Ввести три числа а, b, с. Можно ли представить число а таким образом, чтобы

    	k
    а = х[1]*x[2]*...*x[k] =	П x[i],
    	i=1

    где b <= x[i] <= c; х[i], a, b, c - целые.
    Лучшим считается алгоритм находящий такое представление с наименьшим числом множителей. Предусмотреть вариант, когда такого представления не существует.
13. Возвести число А в натуральную степень n за как можно меньшее количество умножений.
14. Вводятся две последовательности x и y. Найти максимальную по длине последовательность z, которую можно получить вычеркиванием элементов как из x, так и из y. Например, пусть x = 'abacs', y = 'dalas'. Тогда z = 'aas'.
15. Пусть x и y - две бинарных последовательности (т.е. элементы последовательностей - нули и единицы); x и y можно рассматривать как запись в двоичной форме некоторых двух натуральных чисел.
    Найти максимальное число z, двоичную запись которого можно получить вычеркиванием цифр как из x, так и из y. Ответ выдать в виде бинарной последовательности.
16. Полигон.
    Существует игра для одного игрока, которая начинается с задания Полигона с N вершинами. Пример графического представления Полигона показан на рис. 1, где N = 4. Для каждой вершины Полигона задаётся значение - целое число, а для каждого ребра - метка операции +(сложение) либо *(умножение). Ребра Полигона пронумерованы от 1 то N.
    
    Рис. 1. Графическое представление Полигона
    
    Первым ходом в игре удаляется одно из ребер.
    Каждый последующий ход состоит из следующих шагов:
    • выбирается ребро E и две вершины V₁ и V₂, которые соединены ребром E;
    • ребро E и вершины V₁ и V₂ заменяются новой вершиной со значением, равным результату выполнения операции, определенной меткой ребра E, над значениями вершин V₁ и V₂.
    Игра заканчивается, когда больше нет ни одного ребра. Результат игры - это число, равное значению оставшейся вершины.
    Пример игры:
    Рассмотрим Полигон на рис.1. Игрок начал игру с удаления ребра 3 (см. рис 2).
    
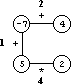
    Рис. 2. Удаление ребра 3
    
    После этого, игрок выбирает ребро 1 (см. рис3), затем - ребро 4 (см. рис 4),
    
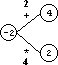
    Рис. 3. Результат выбора ребра 1
    
    
    
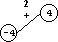
    Рис. 4. Результат выбора ребра 4
    
    и, наконец, ребро 2. Результатом игры будет число 0 (см. рис 5).
    
    Рис. 5. Результат выбора ребра 2.
    
    Напишите программу, которая по заданному Полигону, вычисляет максимальное значение оставшейся вершины и выводит список всех тех ребер, удаление которых на первом ходе игры позволяет получить это значение.
    Входные данные:
    Файл POLIGON.IN описывает Полигон с N вершинами. Файл содержит две строки. В первой строке записано число N. Вторая строка содержит метки ребер с номерами 1, ..., N, между которыми записаны через один пробел значения вершин (первое из них соответствует вершине, смежной ребрам 1 и 2, следующее - смежной ребрам 2 и 3, и так далее, последнее - смежной ребрам N и 1). Метка ребра - это буква t, соответствующая операции +, или буква x, соответствующая операции *.
    Пример входного файла:
    
    4
    t -7 t 4 x 2 x 5
    Данный входной файл описывает Полигон, изображенный на рис. 1.
    Вторая строка начинается с метки ребра 1.
    Выходные данные:
    В первой строке выходного файла POLIGON.OUT программа должна записать максимальное значение оставшейся вершины, которое может быть достигнуто для заданного Полигона. Во второй строке должен быть записан список всех тех ребер, удаление которых на первом ходе, позволяет получить это значение. Номера ребер должны быть записаны в возрастающем порядке и отделяться друг от друга одним пробелом.
    Пример выходного файла:
    
    33
    1 2
    Таким должен быть выходной файл для Полигона, изображенного на рис. 1.
    Ограничения:
    3 < N < 50
    Для любой последовательности ходов, значения вершин находятся в пределах [-32768,32767].
17. "Эпидемия".
    В связи с эпидемией гриппа в больницу направляется А больных гриппом "А" и В больных гриппом "В". Больных гриппом "А" нельзя помещать в одну палату с больными гриппом "В". Имеется информация об общем количестве палат P в больнице, пронумерованными от 1 до P, и о распределении уже имеющихся там больных.
    Написать программу, которая определяет максимальное количество больных M, которое больница в состоянии принять. При размещении новых больных не разрешается переселять уже имеющихся больных из палаты в палату. Спецификация входных данных.
    Входные данные находятся в текстовом файле с именем AMB.IN и имеют следующую структуру:
    • в первой строке находится число A (целое, 0 <= A <= 100);
    • во второй строке - число B (целое, 0 <= B <= 100);
    • в третьей строке - число P (натуральное, P <= 20);
    • в каждой из последующих P строк находятся 3 числа n, a, b, разделенных пробелом где n - вместимость палаты, a - количество уже имеющихся в палате больных гриппом "А", b - количество уже имеющихся в палате больных гриппом "В". Информация о вместимости палат вводится последовательно для палат с номерами 1, 2, ..., P. Числа n, a, b - целые неотрицательные, меньшие 100.
    Спецификация выходных данных.
    
    Выходные данные должны быть записаны в текстовый файл с именем AMB.OUT и иметь следующий формат:
    • в первой строке должно находиться число M;
    • если все поступившие больные размещены, то во второй строке должны находиться номера палат, разделенные пробелом, куда помещаются больные гриппом "А".
    Пример 1:
    входной файл AMB.IN
    10
    7
    3
    5 2 0
    4 0 1
    8 0 0
    выходной файл AMB.OUT
    13
    Пример 2:
    входной файл AMB.IN
    10
    3
    3
    5 2 0
    4 0 1
    8 0 0
    выходной файл AMB.OUT
    13
    1 3
18. Игра.
    Задается натуральное число N (N <= 999). Двое играющих называют по очереди числа, меньшие 1000, по следующим правилам. Начиная с числа N, каждое новое число должно увеличивать одну из цифр предыдущего числа (возможно незначащий нуль) на 1, 2 или 3. Проигравшим считается тот, кто называет число 999. Для заданного N необходимо определить, может ли выиграть игрок, делающий первый ход, при наилучших последующих ходах противника. Вывести сообщение "Первый выигрывает" или "Первый проигрывает". В случае возможности выигрыша первым игроком, требуется напечатать все его возможные первые ходы.
    Входные данные: N
    Выходные данные:
    1. <"Первый выигрывает"> x₁ x₂... x_n, где x₁, ..., x_n - все его возможные первые ходы.
    2. <"Первый проигрывает">
    Пример:
    1. Ввод: 20
       Вывод: "Первый выигрывает" 23 40 320
    2. Ввод: 16
       Вывод: "Первый выигрывает" 19 36 216
19. Треугольник.
    7
    3 8
    8 1 0
    2 7 4 4
    4 5 2 6 5
    Рис. 1
    
    На Рис. 1 показан числовой треугольник. Написать программу, которая определяет максимальную сумму чисел, расположенных на пути, который начинается с верхнего числа и заканчивается на каком-нибудь числе в основании треугольника (максимум суммы среди всех таких путей).
    На каждом шаге можно двигаться к соседнему по диагонали числу влево-вниз или вправо-вниз.
    Число строк в треугольнике > 1 и <= 100
    Все числа в треугольнике - целые в интервале между 0 и 99 включительно.
    Входные данные: Данные о количестве строк в треугольнике находятся в первой строке файла с именем INPUT.TXT. В нашем примере файл INPUT.TXT имеет такой вид:
    5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
    Выходные данные:
    Наибольшая возможная сумма в выходном файле с именем OUTPUT.TXT. В нашем примере: 30.
20. Торговые скидки.
    В магазине каждый товар имеет цену. Например, цена одного цветка равна 2 ICU (ВЕИ - валютные единицы информатики), а цена одной вазы равна 5 ICU. чтобы привлечь покупателей, магазин ввел скидки. Скидка заключается в том, чтобы продавать набор одинаковых или разных товаров по пониженной цене.
    Примеры: три цветка за 5 ICU вместо 6 ICU, или две вазы вместе с одним цветком за 10 ICU вместо 12 ICU.
    Напишите программу, вычисляющую наименьшую цену, которую покупатель должен заплатить за заданные покупки. Оптимальное решение должно быть получено посредством скидок. Набор товаров, который требуется купить, нельзя дополнять ничем, даже если бы это снизило общую стоимость набора. Для описанных выше цен и скидок наименьшая цена за три цветка и две вазы равна 14 ICU: две вазы и один цветок продаются по сниженной цене за 10 ICU и два цветка - по обычной цене за 4 ICU.
    Входные данные.
    Входные данные содержаться в двух файлах: INPUT.TXT и OFFER.TXT. Первый файл описывает покупки ("корзину с покупками"). Второй файл описывает скидки. В обоих файлах содержаться только целые числа. Первая строка файла INPUT.TXT содержит количество b различных видов товара в корзине (0 <= b <= 5). Каждая из следующих b строк содержит значения c, k и p. Значение c - уникальный код товара (1 <= c <= 999). Значение p задает, сколько единиц товара находиться в корзине (1 <= k <= 5). Обратите внимание, что общее количество товаров в корзине может быть не более 5*5=25 единиц.
    Первая строка файла OFFER.TXT содержит количество s возможных скидок (0 <= s <= 99). Каждая из следующих s строк описывает одну скидку, определяя набор товаров и общую стоимость набора. Первое число n в такой строке определяет количество различных видов товара в наборе (1 <= n <= 5). Следующие n пар чисел (c, k) указывают, что k единиц товара с кодом c включены в набор для скидки (1 <= k <= 5, 1 <= x <= 999). последнее число в строке p определяет уцененную стоимость набора (1 <= p <= 9999). Стоимость набора меньше суммарной стоимости отдельных единиц товаров в наборе.
    Выходные данные.
    Запишите в выходной файл OUTPUT.TXT одну строку с наименьшей возможной суммарной стоимостью покупок, заданных во входном файле.
    Пример ввода и вывода.
    Рисунок 1 показывает входные и выходной файлы для приведенного выше примера. Код продукта-цветка равен 7, а вазы - 8.
    

    INPUT.TXT	OFFER.TXT	OUTPUT.TXT
    2	2	14
    7 3 2	1 7 3 5
    8 2 5	2 7 1 8 2 10

    Рисунок 1: Пример ввода и вывода.
21. Больше не запишешь.
    В файловой системе настенного персонального компьютера ВС-1 (Висячая Система) файлы организованы в каталоги.
    В компьютере нет понятия устройства и поэтому полное имя файла является строкой, состоящей из имен каталогов и имени файла, разделенных с символом "\", причем "\" не может быть первым, последним символом, а также идти два раза подряд.
    Имя файла (каталога) может быть произвольной длины, но длина полного имени файла не может быть длиннее N символов. В качестве символов, допустимых к употреблению в именах файлов (каталогов), могут использоваться символы из алфавита, состоящего из K букв (символ "\" не входит в их число). Для данных K (1 <= K <= 13) и N (1 <= N <= 50) определить максимальное число файлов, которое можно записать на данный компьютер.
    Формат ввода: K, N
    Формат вывода: <максимальное количество файлов>
22. Концерт.
    Во вpемя тpансляции концеpта "Стаpые песни о главном - 3" предприниматель К. решил сделать бизнес на производстве кассет. Он имеет M кассет с длительностью звучания D каждая и хочет записать на них максимальное число песен. Эти песни (их общее количество N) передаются в порядке 1, 2, ..., N и имеют заранее известные ему длительности звучания L(1), L(2), ..., L(N). Предприниматель может выполнять одно из следующих действий:
    1. Записать очередную песню на кассету (если она туда помещается) или пропустить ее.
    2. Если песня на кассету не помещается, то можно пропустить песню или начать ее записывать на новую кассету. При этом старая кассета откладывается и туда уже ничего не может быть записано.
    Определить максимальное количество песен, которые предприниматель может записать на кассеты.
    Входные данные записаны в файле KASS.DAT следующим образом. В первой строке файла находятся числа N, M и D. Начиная со второй строки находятся числа L(1), L(2), ..., L(N), по одному в строке. Все числа - натуральные.
    Ответ выдать в файл с именем KASS.OUT
23. Лестница.
    Методист по информатике О. Г. живет на N-ом этаже 9-тиэтажного дома с лифтом, который может останавливаться на каждом этаже. Между соседними этажами дома имеется лестница из двух пролетов, разделенных площадкой, по k ступенек в каждом пролете. Сколькими способами О. Г. может подняться на свой этаж, если поднимаясь по лестнице, можно становиться на следующую ступеньку или через одну ступеньку?
    Ввод c клавиатуры: N, k, где N, k - натуральные, N <= 9, k <= 15
    Вывод на экран: число S
    Время тестирования каждой задачи ограничено. Все входные данные корректны.
24. Подряд идущие единицы.
    Среди всех N-битных двоичных чисел указать количество тех, у которых в двоичной записи нет подряд идущих k единиц. Сами числа выдавать не надо! N и k - натуральные, k <= N <= 30. Данные корректны.
    Ввод:
    <N => N
    <k => k
    Вывод:
    <Количество чисел => количество
    Пример:
    N=3
    k=2
    Количество чисел = 5.
    Действительно, среди всех 3-битных чисел 000, 001, 010, 011, 100, 101, 110, 111 есть 5 чисел 000, 001, 010, 100, 101, у которых в записи 2 единицы не идут подряд.
25. "Юбилей"
    В связи с открытием олимпиады-98 по информатике в Могилеве N человек (N <= 10) решили устроить вечеринку. Для проведения вечеринки достаточно купить MF бутылок фанты, MВ бананов и MC тортов. Требуется определить минимальный взнос участника вечеринки. При покупке определенных наборов товара действует правила оптовой торговли: стоимость набора товара может отличаться от суммарной стоимости отдельных частей.
    Написать программу, которая по входным данным определяет минимальный взнос участника вечеринки.
    Входные данные находятся в текстовом файле с именем PART.IN и имеют следующий формат:
    • в первой строке находятся числа N (количество человек, <= 10) и M (количество возможных наборов, <=100000);
    • в каждой из следующих M строк находятся 4 числа: F,B,C,S где F,B,C - количество бутылок фанты, штук бананов и тортов в наборе (0 <= F, B, C <= 1000), а S - стоимость набора (S <= 100000).
    в последней строке находятся числа MF, MB и MC (MF, MB, MF <=9).
    Выходные данные должны находится в текстовом файле с именем PART.OUT и содержать число V - минимальный взнос участника.

    Главная

    Предыд.

    След.

    Др. раздел