Будем использовать следующие процедуры, необходимые для реализации основных операций в структуре данных d-куча. Процедура Swap(i, j) меняет местами ключи вершин i и j. Например, для d-кучи (d = 2), представленной массивом

i	0	1	2	3	4	5	6	7
dHeap[i]	5	6	7	4	8	11	12	9

применим процедуру swap(4, 6)

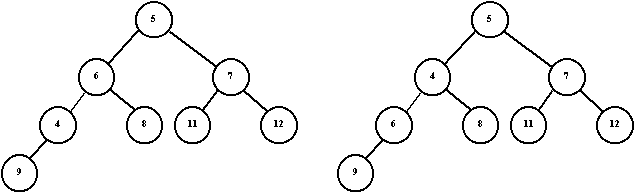
Пример кучи перед перестановкой swap(4, 6) и после проведенной перестановки.

Псевдокод процедуры Swap(i, j):

procedure Swap(i, j);
begin
k := key[i];
key[i] := key[j];
key[j] := k;
end;

Трудоемкость процедуры Swap(i, j) есть O(1).

В процессе работы над d-кучей часто требуется менять значения ключей, переставлять элементы. При этом может временно нарушаться основное свойство кучи (инвариант 1).

i-ой вершины key[i] и и пусть j = Pred[i]. Тогда могут возникнуть два случая:

• key[j] < key[i], т.е. инвариант 1 выполнен;
• key[j] > key[i], т.е. инвариант 1 нарушен и мы должны его восстановить.

Эту задачу выполняет процедура SiftUp(i):

procedure SiftUp(i);
begin
while (i <> root) and (key[i] < key[Pred[i]]) do
{
Swap(i, Pred[i]);
i := Pred[i];
}
end;

Процедура SiftUp(i) имеет трудоемкость O(log_dn), т.к. после каждой итерации цикла уменьшается глубина узла i, а согласно свойству d-дерева, его начальная глубина – O(log_dn).

Предположим далее, что мы увеличили ключ некоторой вершины i. Возможны два случая:

• если после изменения key[i] <= key[j], для всех j из Succ(i), то инвариант 1 выполнен;
• key[i] > key[j], то необходимо восстановить основное свойство кучи (инвариант 1). Это можно сделать, применив процедуру SiftDown(i):

procedure SiftDown(i);
begin
while (i <> leaf) and (key[i] > key[minchild(i)]) do
{
Swap(i, minchild(i));
i := minchild(i);
}

Процедура SiftDown(i) требует O(d log_dn) операций, т.к. на поиск листа затрачивается O(log_dn) операций, а вычисление minchild(i) требует O(d) операций.

Покажем, что для d-кучи основные операции могут быть реализованы с помощью процедур SiftUp(i), SiftDown(i), Swap(i, j).

Основными операциями над d-кучей являются следующие:

• find_min(i, dHeap) найти элемент i с минимальным ключом в куче;
• insert(i, dHeap) – вставить элемент i в кучу;
• delete_min(i, dHeap) – удалить элемент i с минимальным ключом из кучи.

Нахождение вершины с минимальным ключом find_min(i, dHeap).

Эта операция находит вершину с минимальным ключом. Она находится в корне, а поскольку d-куча представлена в виде массива, то минимальный элемент находится в позиции с индексом 0. Для нахождения вершины с минимальным ключевым значением необходимо выполнить O(1) операций в наихудшем случае.

Вставка элемента в d-кучу insert(i, dHeap).

Эта операция осуществляет вставку новой вершины i в d-кучу путем добавления новой вершины в конец массива dHeap[i], i = 0, ..., last, где last – индекс последнего элемента перед вставкой новой вершины i в d-кучу, т.е. dHeap[last] := key[i], после чего last надо увеличить на 1. Поскольку добавление новой вершины может нарушить инвариант 1, то восстанавливаем его с помощью процедуры SiftUp(i).

procedure insert(i, dHeap)
begin
dHeap[last] := key[i];
last := last + 1;
SiftUp(last);
end;

Трудоемкость этой операции O(log_dn).

Удаление минимального элемента из d-кучи. Операция delete_min(i, dHeap).

Удаление будем производить следующим образом: меняем первый элемент d-кучи (минимальный элемент) с последним и уменьшаем размерность d-кучи на 1. Такая замена может нарушить инвариант 1. Для восстановления инварианта 1, начиная с корневой вершины двигаемся по единственному пути до некоторой вершины k, для которой инвариант 1 выполнен. Это производится с помощью процедуры SiftDown(i), i = root. Псевдокод процедуры удаления минимального элемента из d-кучи:

procedure delete_min(i, dHeap)
begin
Swap(root, last);
last := last - 1;
SiftDown(root);
end;

Трудоемкость этой процедуры O(log_dn).

Наряду с основными операциями в d-куче часто рассматриваются операции:

• Удаление произвольного элемента из кучи.
  Для этого необходимо знать адрес (индекс) этого элемента. Операция delete(i, dHeap) удаляет из кучи произвольный элемент, соответствующий вершине i. Для удаления поступаем следующим образом. Положим key[i] := key[root]-1. С помощью процедуры SiftUp(i) обеспечиваем основное свойство кучи. Далее применим операцию delete_min(i dHeap) для удаления из d-кучи элемента с минимальным ключом key[root]-1.
• Уменьшение ключа вершины i на значение value: decrease_key(i, value, dHeap).
  Если после выполнения операции нарушен инвариант 1, то восстанавливаем его с помощью процедуры SiftUp(i).
• Увеличение ключа вершины i на значение value: increase_key(i, value, dHeap).
  Увеличиваем значение ключа вершины i на заданное значение value и если нарушен инвариант 1, то применяем процедуру SiftDown(i).