- Поиск минимального элемента
- Слияние двух биномиальных куч
- Добавление нового элемента в кучу
- Создание биномиальной кучи
- Удаление минимального элемента
Эта процедура требует проверки корневых значений всех биномиальных деревьев кучи. Для эффективной реализации данной процедуры необходимо, чтобы структура данных, используемая для хранения биномиальной кучи, обеспечивала быстрый доступ к корневым значениям всех биномиальных деревьев (например, корневые вершины всех биномиальных деревьев объединены в связный список). Так как количество деревьев есть O(log n), то трудоемкость алгоритма поиска минимального элемента есть O(log n).
Слияние предполагает получение из двух биномиальных куч H1 и H2 новой биномиальной кучи H3. Будем предполагать, что мы поддерживаем для каждой биномиальной кучи упорядоченность биномиальных деревьев по их высотам, что позволит выполнить процесс слияния более эффективно.
Рассмотрим процесс слияния двух куч, представленных на рисунке:
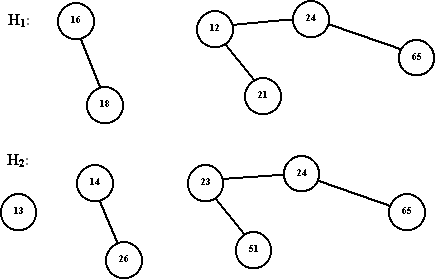
- Так как биномиальная куча H2 содержит дерево высоты 0, а H1 – нет, то добавляем это дерево в кучу H3.
- Так как обе биномиальные кучи H1 и H2 содержат деревья высоты 1, то сливаем эти деревья, полагая корень с большим корневым значением одним из сыновей корня с меньшим корневым значением. В результате получаем биномиальное дерево высоты h = 2. Таким образом, новая куча не будет иметь биномиального дерева высоты 1.
- Так как сейчас имеется три биномиальных дерева высоты h = 2 (по одному в H1 и H2 и полученное на предыдущем этапе слияния), то одно из них мы помещаем в кучу H3, а два других сливаем и получаем дерево высоты h = 3.
- Так как ни одна из куч H1 и H2 не имеет дерева высоты h = 3, то помещаем полученное дерево в кучу H3 и завершаем процесс слияния.
- каждая вершина содержит информацию о ее высоте;
- биномиальные деревья упорядочены по высотам;
- каждая вершина имеет указатель на первого сына (nil, если сыновей нет), указатели на левого и правого брата;
- сыновья каждой вершины представлены в виде двухсвязного списка и упорядочены по размерам их поддеревьев, указатель левого брата первого сына есть последний сын.
Для эффективного выполнения процедуры слияния двух биномиальных куч необходимо, чтобы структура данных, разработанная для хранения биномиальной кучи, имела следующий вид:
С учетом разработанной структуры данных, процесс слияния двух биномиальных деревьев выполняется за константное время.
Очевидно, что данная процедура может рассматриваться как частный случай процедуры слияния. Создадим одноэлементную кучу, состоящую из единственного биномиального дерева B0 и выполним процедуру слияния. Трудоемкость процедуры добавления нового элемента в кучу есть O(log n).
Предположим, что нам необходимо создать биномиальную кучу из n элементов. Тогда одним из возможных вариантов решения является вызов n раз процедуры добавления элемента в кучу. В этом случае трудоемкость процедуры создания кучи есть O(n), хотя следовало бы ожидать оценку порядка O(n log n). Для этого отметим, что если в уже созданной куче наименьшее по высоте не существующее дерево есть Bi, то время добавления элемента в кучу пропорционально i + 1. Для примера, если в куче H3 не существует дерева высоты 1, то процедура добавления нового элемента будет осуществлена за два шага (образование кучи из одного единственного элемента плюс слияние с уже существующим деревом высоты 1).
Будем предполагать, что биномиальная куча реализована в виде структуры, описанной ранее для операции слияния двух биномиальных куч.
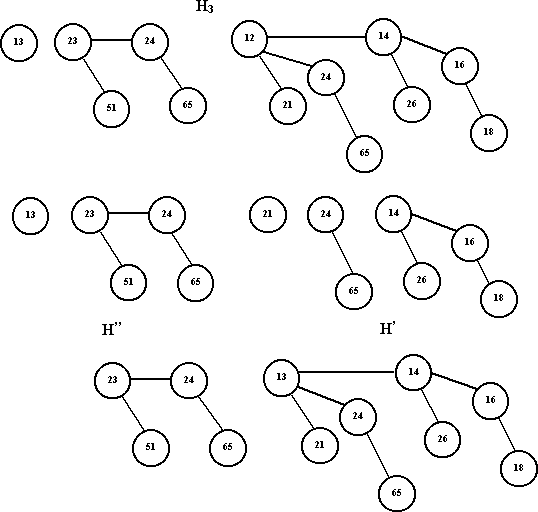
- Для выполнения процедуры удаления минимального элемента необходимо сначала найти биномиальное дерево с минимальным корневым значением. Предположим, что это дерево Bk. Трудоемкость этого шага алгоритма есть O(log n).
- Удаляем дерево Bk из кучи H, формируя новую биномиальную кучу H' (куча H без дерева Bk). Трудоемкость этого шага алгоритма есть O(1).
- Удаляем из дерева Bk корень, в результате чего бинарное дерево Bk распадается на деревья B0,B1, ..., Bk, из которых мы образуем новую биномиальную кучу H". Трудоемкость этого шага алгоритма есть O(1).
- Выполняем операцию слияния куч H' и H". Трудоемкость слияния двух куч есть O(log n).
Следовательно, трудоемкость процедуры удаления минимального элемента есть O(log n).
Ниже показана куча, полученная из кучи H3 после удаления из нее минимального элемента (12).
Анализ основных процедур работы с биномиальными кучами приводит к следующей структуре данных для представления биномиальной кучи:
type
tree_ptr = ^tree_node;
tree_node = record
element: integer;
rank: integer;
f_child: tree_ptr;
l_sib: tree_ptr;
r_sib: tree_ptr;
end;
PRIORYTY_QUEUE = tree_ptr;
Таким образом, каждый элемент, описанной выше мультисписковой структуры, содержит следующую информацию: ключевое значение вершины, количество сыновей (которое называется рангом вершины), указатель на первого сына, указатель на левого и правого брата. Сыновья каждой вершины представлены в виде двухсвязного списка и упорядочены по размерам их поддеревьев, указатель левого брата первого сына есть последний сын.
Приведем программную реализацию процедуры слияния двух биномиальных куч.
function merge_tree(T1, T2 : PRIORITY_QUEUE): PRIORITY_QUEUE;
begin
if T1 ^.element > T2 ^.element then swap(T1; T2);
if T1 ^.rank = 0 then T1 ^.f _child := T2;
else
{
T2 ^.l_sib := T1 ^.f _child^.l_sib;
T2 ^.l_sib ^.r_sib := T2;
T1 ^.f _child ^.l_sib := T2;
}
T1 ^.rank := T1 ^.rank + 1;
merge_tree := T1;
end;
function merge(H1, H2 : PRIORITY_QUEUE) : PRIORITY_QUEUE;
var H2 : PRIORITY_QUEUE;
T1, T2, T3 : PRIORITY_QUEUE;
begin
if H1 = nil then merge := H2
else
if H2 = nil then merge := H1
else
if H1 ^.rank < H2 ^.rank then
{
extract(T1, H1); H3 := merge(H1, H2);
T1 ^.l_sib := H3 ^.l_sib;
H3 ^.l_sib: ^.r_sib := nil;
T1 ^.r_sib := H3; H3 ^.l_sib := T1; merge := T1;
}
else
if H2 ^.rank < H1 ^.rank then merge := merge(H2, H1)
else
{
extract(T1, H1); extract(T2, H2);
H3 := merge(H1, H2); T3 := merge_tree(T1, T2);
merge := merge(H3, T3);
}
end;
Приведенная выше функция слияния двух куч merge(H1,H2 : PRIORITY_QUEUE)
использует функцию слияния двух биномиальных деревьев
merge_tree(T1, T2 : PRIORITY_QUEUE)
и предполагает, что существует функция extract(T, H), которая
удаляет дерево T из биномиальной кучи H.