Полным бинарным деревом называется такое дерево, в котором каждая вершина имеет не более двух "сыновей", а заполнение вершин осуществляется впорядке отверхних уровней к нижним, причем на одном уровне заполнение вершин производится слева направо.

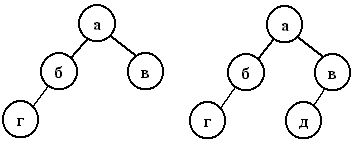
a) полное бинарное дерево; b) неполное бинарное дерево

На рисунке a) изображено полное бинарное дерево, которое имеет три уровня. На втором уровне находится только одна заполненная вершина (a), которая называется корневой. На первом уровне заполнены две вершины (б,в), на нулевом уровне заполнена одна (г). Дерево b) не является полным бинарным деревом, так как заполнение вершин уровня 0 осуществлялось не слева направо (не заполнена вершина между вершинами "г" и "д"). Нетрудно убедиться, что в дерево a) можно добавить (заполнить) максимум три вершины, чтобы количество уровней в нем не изменилось. Если мы добавим (заполним) четыре вершины, то получится полное четырехуровневое бинарное дерево, которое изображено на рисунке:

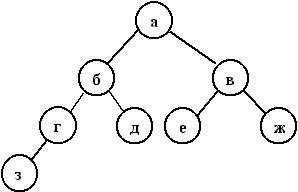
Полное четырехуровневое бинарное дерево.

Очевидно, что минимальное количество вершин в полном трехуровневом бинарном дереве равно 4, а максимальное в полностью заполненном – 7.